De saltos, velocidades, y Red Bull

Vamos a empezar con un poquitín de física básica, de la que se estudiaba en el colegio. Espero que nadie se asuste y abandone nada más empezar.

Newton nos enseñó que un cuerpo, dejado a sí mismo sin ninguna fuerza actuando sobre él, se queda en reposo o se mueve con velocidad constante. Aunque parezca sencillo, en nuestra experiencia diaria es difícil observar esto, porque siempre hay una fuerza actuando sobre nosotros: la atracción gravitatoria de la Tierra, es decir nuestro propio peso. Además, en cuanto ponemos algo en movimiento, el rozamiento con el suelo o con el aire tiende a frenarlo. Pero la genial abstracción del movimiento libre que tuvo Newton es válida, y la aceptamos sin demasiados problemas.

Por el contrario, cuando ejercemos una fuerza sobre ese cuerpo en reposo, se acelera. Si la fuerza es constante, la aceleración también lo es, lo que se manifiesta como un continuo aumento de la velocidad. Los físicos expresamos esto usando la relación entre la velocidad ( v ), la aceleración ( a ) y el tiempo ( t ) que dice que v = a • t , es decir, la velocidad se obtiene multiplicando la aceleración por el tiempo durante el que actúa.

Un caso que estudiábamos en la escuela es el de la “caída de graves”: aquí la aceleración constante es la de la gravedad, que la Tierra ejerce sobre todos los cuerpos, y provoca un aumento en la velocidad de 9,8 metros por segundo cada segundo que pasa. Así, si un cuerpo se deja caer desde una cierta altura y cae durante un segundo, habrá alcanzado una velocidad de 9,8 metros por segundo (m/s, para abreviar). Como no estamos muy acostumbrados a esas unidades, señalo que 10 m/s son exactamente 36 km/h, algo más familiar.

En el colegio aplicábamos estas fórmulas con gran alegría, y si nos pedían la velocidad a la que caería un cuerpo tras 20 segundos de caída (una buena caída, eso es cierto) pues responderíamos tranquilamente que sería v = a • t = 20 • 9,8 = 196 m/s. Sin problema, profe, póngame el siguiente que esto lo domino…Pero claro… pensando un poco, resulta que 196 m/s son 706 km/h. Eso es un poco rápido… a esa velocidad (incluso a velocidades mucho menores) deberíamos tener en cuenta que el problema es más complicado: el aire ejerce resistencia por rozamiento, y frena la caída. Como todos hemos visto en la realidad, no cae igual de rápido un papel que una piedra, y los coches de carreras (¡y todos los demás!) se hacen aerodinámicos por algo. Si uno tiene en cuenta todos esos factores, descubre que hay una velocidad límite a la que puede caer un cuerpo en la atmósfera terrestre. A esa velocidad la resistencia del aire es ya tan fuerte que compensa el propio peso, por tanto no hay aceleración ninguna, y la velocidad permanece constante.

Esa velocidad se llama velocidad terminal y para un cuerpo en la atmósfera baja de la Tierra es de aproximadamente 200-300 km/h, dependiendo de su forma exacta. Lo interesante es que esa velocidad prácticamente se alcanza al cabo de unos 15 segundos. Es decir, independientemente de la altura original, un cuerpo que cae durante más de 15 segundos llegará con la misma velocidad al suelo (ver Figura 1, arriba).

Hay que insistir en que esto ocurre porque estamos en el mundo real, y la Tierra tiene una atmósfera gaseosa. En ausencia de atmósfera todos los cuerpos caen a la misma velocidad, como se puede comprobar de modo espectacular en este vídeo.

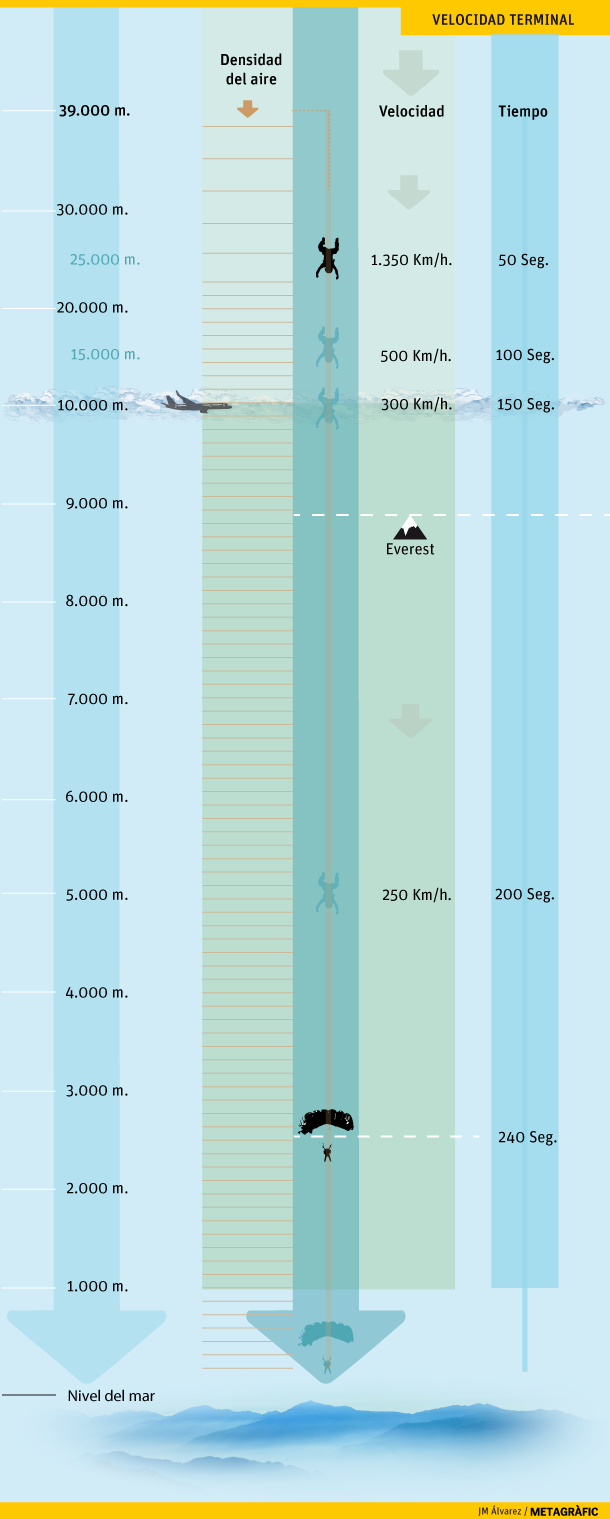
Y ahora… sí, por supuesto, voy a hablar de Felix Baumgartner y su salto estratosférico del día 14 de octubre de 2012, patrocinado por una famosa marca de bebidas energéticas. Felix saltó desde una altura de 39 000 metros, y cayó durante cuatro minutos y dieciseis segundos antes de abrir su paracaídas. Nuestro ingenuo cálculo permitiría calcular para esa caída de 256 segundos una velocidad de 256 • 9,8 = 2510 m/s = 9030 km/h en el momento de abrir el paracaídas, pero por supuesto sabemos que está equivocado–y menos mal, pensarían el pobre Felix y su paracaídas…

En realidad la alta atmósfera, donde inició su salto, es tremendamente ligera, con una densidad de aire menor a una centésima parte de la que tenemos al nivel del mar. Por tanto la resistencia es inicialmente ínfima, y durante bastantes segundos realmente la aceleración era casi constante. Por eso pudimos observar sorprendidos en la televisión como la velocidad de Felix crecía muy rápidamente en los primeros momentos de su caída. De hecho su velocidad se estabilizó al cabo de unos 45 segundos. Ahora que sabemos términos físicos, podemos decir que “a los 45 segundos alcanzó la velocidad terminal”, que, a esa altura, era de casi 1350 km/h (En Figura 1, abajo, podemos ver un modelo de su caída).

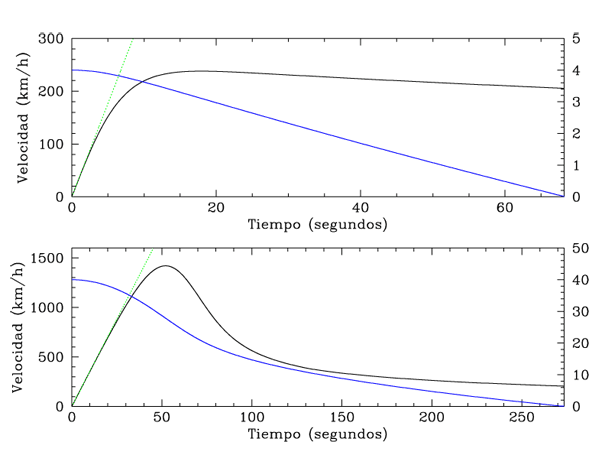
Figura 1: Modelo de la caída de un cuerpo desde una altura de 4000 metros (arriba) y de 40 000 metros (abajo). En cada caso la línea azul muestra la altura en cada momento (eje de la derecha, en kilómetros), y la línea negra la velocidad (eje de la izquierda). La línea verde punteada indica cómo cambiaría la velocidad en ausencia del rozamiento del aire. Se puede comprobar que en el caso de una caída desde la altura de 4000 metros el rozamiento del aire se hace notar ya a los 10 segundos, y se alcanza la velocidad límite (de poco más de 200 km/h) al cabo de unos 15 segundos. En cambio, en un salto estratosférico como el de Felix Baumgarten el efecto del aire es apenas notable hasta los 40 segundos, cuando ya se han superado los 1000 km/h.

.

Curiosamente entonces se produjo otro efecto interesante. Felix avanzaba a gran velocidad (de hecho, a velocidad supersónica, lo que era uno de sus objetivos) hacia zonas más densas de la atmósfera. Por tanto, cada vez se encontraba con más resistencia y su velocidad empezó a disminuir rápidamente, en vez de aumentar! Después de los primeros 50 segundos aproximadamente, su velocidad bajó desde los 1350 km/h hasta acercarse a la velocidad terminal de la baja atmósfera, los ya nombrados 250 km/h. Aproximadamente a 2500 metros de altura, tras haber descendido durante más de cuatro minutos, abrió su paracaídas y bajó, “tranquilamente”, hasta la superficie de la Tierra.

Dejando aparte la dinámica de la caída, pero sin salir de la Física, ha habido bastante discusión sobre la cuestión de si la caída superó la velocidad del sonido o no. La velocidad del sonido en el aire a nivel del mar es de poco más de 1200 km/h, y depende sobre todo de la temperatura. En la alta atmósfera la temperatura es menor (aunque no demasiado) y, por tanto, también la velocidad del sonido es menor–aproximadamente de unos 1100 km/h. En cualquier caso, si se confirma que Felix Baumgartner superó en su caída los 1300 km/h, queda fuera de discusión que alcanzó velocidades supersónicas.

No queda claro en cambio cuáles serían los efectos y si se podría haber apreciado un “boom” sónico en el momento en que Felix superó el límite de la velocidad del sonido. El propio saltador reconoce que en ese momento se encontraba demasiado ocupado intentando saber dónde tenía la cabeza como para fijarse en esos detalles. “Red Bull te da alas”, pero incluso con ellas, a algunas velocidades te puedes marear…

1- Cabe recordar aquí también la diferencia entre nuestra masa (que es un valor independiente de donde nos encontremos, y que nos indica la cantidad de materia a la que nos referimos) y nuestro peso, que es la atracción de la Tierra sobre esa masa, y que por supuesto variaría si estuvieramos en la Luna o en otro planeta, y sería cero en el espacio.
2- http://nssdc.gsfc.nasa.gov/planetary/image/featherdrop_sound.mov

© 2012 Conec. Todos los derechos reservados.