El misterio del porqué cuanto más pequeño, más hambre

Acaba de culminar una jornada de senderismo por el bosque, 15 km de cuestas y sendas, y ha llegado a su destino, un típico pueblecito de montaña. Y lo primero que hace es entrar en el bar de la plaza y pedirse unas tapas porque tiene hambre. O bien ha pasado una noche al raso viendo una lluvia de estrellas, resguardándose del frío con relativo éxito pues la ropa que ha escogido quizá no era la más adecuada, y cuando vuelve al hotel se acerca a la chimenea para calentarse y pide algo de comer porque está hambriento. Esto sucede porque tanto el ejercicio físico como el mantener caliente el cuerpo consumen grandes cantidades de energía, energía que recuperamos a través de la comida; por ello en verano, cuando estamos de vacaciones y nuestra principal ocupación es descansar, solemos tener menos hambre.

Aún así, por muy cómodos que estemos y por poco que nos movamos, el cuerpo sigue consumiendo energía. Este gasto energético mínimo imprescindible para mantener las funciones básicas es lo que se conoce por metabolismo basal. En animales se mide con éstos en reposo y una vez que han pasado 12 horas de su anterior comida, pues los procesos digestivos también implican un gasto energético adicional. Se mide además en condiciones de termoneutralidad, es decir, a una temperatura que no les resulte ni fría ni caliente, para evitar un consumo extra de energía bien sea para mantenerse caliente bien sea para refrescarse. Hay además dos maneras de medirlo, o por calorimetría directa, midiendo cuánto calor genera el individuo, o indirecta, midiendo el consumo de oxígeno y asumiendo que ambos métodos deben dar el mismo resultado. En el caso de una persona adulta de unos 70 kg, el metabolismo basal corresponde a unos 70 vatios, con lo que 30 personas en una habitación vienen a generar el mismo calor que una estufa de 2000 vatios.

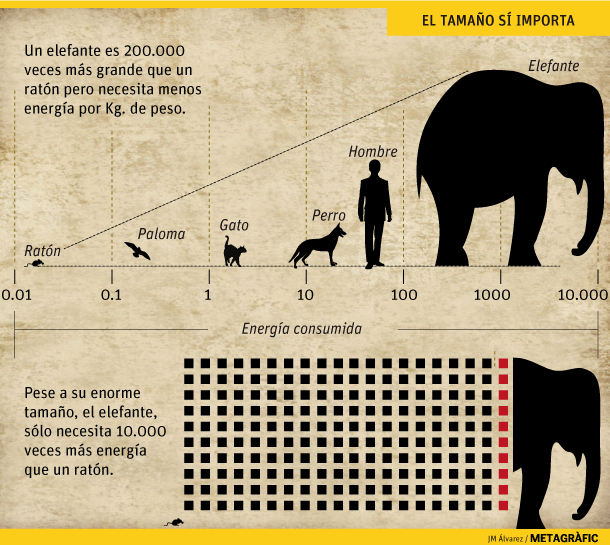
Un animal pequeño y uno grande no consumen lo mismo, y en primera aproximación parece lógico suponer que si un animal pesa el doble que otro, también consumirá el doble de energía, ya que tiene el doble de células que alimentar. Es decir que el metabolismo basal sea directamente proporcional a la masa. Pero en realidad las cosas son más complicadas. El consumo energético por cada kilo de masa resulta ser mayor cuanto más pequeño es el animal. Por ejemplo, en proporción a su peso, un ratón consume energía a un ritmo 70 veces mayor que un ser humano. El primero en observar este curioso fenómeno fue Max Rubner en 1883, midiendo el metabolismo de perros de diferente tamaño, pero ¿cuál es su causa?

Las primeras explicaciones achacaban el fenómeno a las pérdidas por calor, que son proporcionalmente mayores cuanto más pequeño es el organismo. Esto se debe a la ley cuadrático-cúbica que ya enunciara de Galileo, y es fácil de ver si me permiten un poco de matemáticas. La masa es proporcional al volumen, es decir, al cubo de su tamaño, M~L³, y por tanto L~M^1/3. Pero la superficie de su piel, que es por donde se escapa el calor, crece sólo con el cuadrado del tamaño, S~L², y dado que L~M^1/3, sustituyendo obtenemos S~M^2/3. Es decir, la superficie es proporcional a la masa elevada a 2/3, y como la pérdida de calor es proporcional a la superficie, a una patata asada de gran tamaño le será más difícil enfriarse que a una pequeña. Este sencillo razonamiento termodinámico llevó a concluir que si las pérdidas de calor por la piel son la causa última de la dependencia del metabolismo con la masa, el metabolismo basal debería venir dado por una ley de potencias de exponente 2/3.

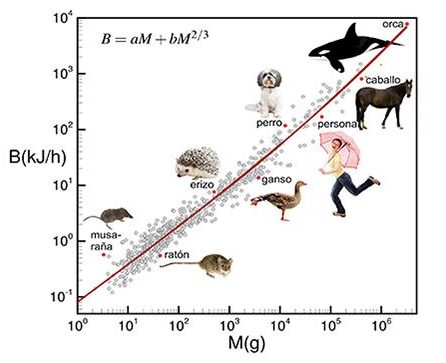
Pero Max Kleiber en 1932, con una muestra amplia de medidas de metabolismo basal, vio que los datos parecían encajar mejor con la masa elevada a una potencia de 3/4 en vez de 2/3. Este inesperado resultado propició una intensa búsqueda de explicaciones alternativas del origen del metabolismo basal, así como un vivo debate entre los defensores del exponente 2/3 y los del 3/4 que duró varias décadas. Hay que tener en cuenta que la diferencia relativa entre ambos valores no es muy alta, sólo un 12%, con lo que junto a la dificultad de obtener datos precisos que permitieran discriminar entre ambos valores (y la medida del metabolismo basal de un animal es ciertamente laboriosa) no había forma de cerrar el debate. Hasta que Geoffrey West y colaboradores elaboraron en 1997 un modelo matemático con el que aparentemente le ponían fin. Este modelo se basa en que la red de suministros del organismos (vasos sanguíneos, bronquios, etc…) es el verdadero factor limitante del funcionamiento del organismo, y por tanto del metabolismo. Y esta red tiene una estructura fractal cuya superficie exterior escala con el volumen justamente como una potencia 3/4.

Este influyente artículo publicado en la revista Science, logró elevar en cierta forma el resultado empírico de Kleiber al rango de ley. Pero conforme se realizaban nuevas medidas y se mejoraba la precisión, la explicación fractal comenzó a hacer agua. Los resultados empíricos acumulados cuestionaban la validez universal del exponente 3/4 al encontrarse clases animales que encajaban mejor con otros exponentes, oscilando entre 1 (como en los insectos) y 2/3 (en el caso de las aves). Y en el caso mejor conocido, el de los mamíferos, al recopilarse datos para un mayor rango de masas (desde musarañas a ballenas) se descubría que el metabolismo basal no seguía en realidad una ley de potencias pura. De haber sido así, al representar esos datos en escala log–log deberían ser una línea recta con pendiente 3/4, pero sin embargo muestran una clara curvatura. Por ejemplo, cuando nos restringimos a mamíferos de menos de 1 kg los datos cuadran mucho mejor con un exponente de 2/3, y para masas por encima de 50 kg el exponente se acerca a 6/7.

Estos resultados que ponen en entredicho el modelo de West han provocado la aparición de una plétora de nuevos modelos para explicar tales discrepancias, algunos de ellos modificaciones del modelo original de West, otros, modelos aptos para casos particulares o ajustes ad hoc sin un claro respaldo biológico, muchos otros, modelos realmente creativos aunque de complejidad creciente o con demasiados parámetros libres. La pérdida del marco de referencia maestro que parecía ser el modelo fractal de West ha dejado un terreno abonado para un nuevo debate sobre el origen de la (ahora incorrectamente llamada) ley de Kleiber, y mucho trabajo pendiente para la navaja de Okcham. Es necesario un nuevo marco de referencia que sea parsimonioso y ayude a reconciliar resultados tan diversos.

El modelo que nuestro equipo publicó recientemente en Scientific Reports pretende ser ese nuevo marco de referencia. En cierta forma es un retorno a la explicación térmica como causa última del fenómeno. Con una diferencia: un organismo no puede utilizar toda la energía que consume en generar calor, una fracción debe ir a “cosas útiles”, como la síntesis de proteínas, la división celular, los latidos cardiacos… es decir, a hacer funcionar y mantener al organismo. Si toda la energía consumida se transformara en calor, ciertamente el metabolismo encajaría con un exponente 2/3, pero entonces no hablaríamos de un organismo sino de una estufa. Por otro lado, si toda la energía se consumiera eficientemente, el metabolismo sería directamente proporcional al número de células que se están alimentando, es decir a la masa M, pero inevitablemente una parte se pierde como calor. En los organismos reales se dan ambos fenómenos, y éstos interpolan entre esos dos extremos ideales, cada factor ponderado por un peso en función de su importancia. Es decir: B = aM + bM^2/3.

Este modelo permite realizar diversas predicciones. Para endotermos de masas bajas, el término con exponente 2/3 domina, lo que explica por qué los mamíferos de pequeño tamaño y las aves (también pequeñas) encajan mejor con este exponente. En cambio para masas grandes es el otro término el que domina y el exponente se acerca más a 1. Por otro lado los mamíferos polares tienden a ser termodinámicamente ineficientes a fin de mantenerse caliente (a través del uso de proteínas como la termogenina) dando un valor de b más elevado. Y en efecto, los animales polares encajan mejor con un exponente de 2/3. En cambio b es bajo si la diferencia de temperatura entre el entorno y el cuerpo es pequeña, como en el caso de los ectotermos, lo que produce que el primer término sea el dominante y encajen mejor sus datos con exponentes más cercanos a 1.

El modelo también permite hacer predicciones cuantitativas: a partir de argumentos meramente termodinámicos, en nuestro artículo estimamos que para mamíferos la fracción de la ingesta de energía que no se pierde como calor es en promedio de un 21%. Por otro lado sabemos que la síntesis de ATP a partir de glucosa (el proceso dominante en las condiciones bajo las que se mide el metabolismo basal) sólo captura el 42% de la energía, perdiéndose el resto por calor, y el posterior uso de ATP en reacciones biológicas pierde otro 50% de ese 42%, lo que da finalmente un consumo eficiente de un 21%, coincidiendo con la predicción de nuestro modelo. Como esa es la fracción que no se emite como calor, uno esperaría ver tal diferencia entre la calorimetría directa (que mide la producción de calor) y la calorimetría indirecta (consumo de oxígeno), aunque rara vez se toman ambas medidas a la vez. Sin embargo Alexander Zotin publicó en 2010 varias mediciones conjuntas de calorimetría directa e indirecta, a partir de las cuales vemos que estas diferencias oscilan entre el 13 y el 25%, de acuerdo con nuestras predicciones.

¿Es este modelo la explicación definitiva al porqué varía como varía el metabolismo con la masa? Tal vez. Como decíamos, hay otras muchas explicaciones alternativas. Y no necesariamente son mutuamente excluyentes; probablemente muchas de ellas serán válidas dentro de ciertos límites. Pero nuestro modelo de balance entre consumo eficiente y pérdida térmica es autoconsistente, se basa en principios termodinámicos simples pero sólidos y genera predicciones que explican cuantitativa y cualitativamente toda una serie de características biológicas relevantes. Es un marco general sobre el cual todas las piezas parecen por fin encajar.