El misteri del porquè com més menut, més fam

Acaba de culminar una jornada de senderisme pel bosc, 15 km de costes i sendes, i ha arribat a la seua destinació, un típic poblet de muntanya. I la primera cosa que fa és entrar al bar de la plaça i demanar-se unes tapes perquè té fam. O bé ha passat una nit al ras veient una pluja d’estreles, resguardant-se del fred amb relatiu èxit perquè la roba que ha triat potser no era la més adequada, i quan torna a l’hotel s’acosta a la llar per a calfar-se i demana alguna cosa per a menjar perquè té gana. Açò ocorre perquè tant l’exercici físic com mantenir calent el cos consumeixen grans quantitats d’energia, energia que recuperem a través del menjar; per això a l’estiu, quan estem de vacacions i la nostra principal ocupació és descansar, solem tenir menys fam.

Tot i això, per molt còmodes que estiguem i per poc que ens moguem, el cos continua consumint energia. Aquesta despesa energètica mínima imprescindible per a mantenir les funcions bàsiques és el que es coneix com a metabolisme basal. En animals es mesura quan estan en repòs i una vegada hagen passat 12 hores des de la seua anterior menjada, perquè els processos digestius també impliquen una despesa energètica addicional. Es mesura a més en condicions de termoneutralitat, és a dir, a una temperatura que no els resulte ni freda ni calenta, per a evitar un consum extra d’energia, bé siga per a mantenir-se calent bé siga per a refrescar-se. Hi ha a més dues maneres de mesurar-ho, o per calorimetria directa, mesurant quanta calor genera l’individu, o indirecta, mesurant el consum d’oxigen i assumint que ambdós mètodes han de donar el mateix resultat. En el cas d’una persona adulta d’uns setanta quilos, el metabolisme basal correspon a uns setanta watts, amb la qual cosa trenta persones en una habitació generen la mateixa calor que una estufa de 2.000 watts.

Un animal menut i un de gran no consumeixen el mateix, i en una primera aproximació sembla lògic suposar que, si un animal pesa el doble que un altre, també consumirà el doble d’energia, ja que té el doble de cèl·lules a alimentar. És a dir, que el metabolisme basal siga directament proporcional a la massa. Però en realitat les coses són més complicades. El consum energètic per cada quilo de massa resulta ser més gran com més menut és l’animal. Per exemple, en proporció al seu pes, un ratolí consumeix energia a un ritme setanta vegades més gran que un ésser humà. El primer que va observar aquest curiós fenomen fou Max Rubner en 1883, que va mesurar el metabolisme de gossos de diferent grandària. Però quina és la seua causa?

Les primeres explicacions atribuïen el fenomen a les pèrdues per calor, que són proporcionalment més grans com més xicotet és l’organisme. Açò és degut a la llei quadraticocúbica que ja va enunciar Galileu, i és fàcil de veure si em permeten un poc de matemàtiques. La massa és proporcional al volum, és a dir, al cub de la seua mida, M~L³, i per tant L~M^1/3. Però la superfície de la seua pell, que és per on s’escapa la calor, creix només amb el quadrat de la mida, S~L², i atés que L~M^1/3, substituint obtenim S~M^2/3. És a dir, la superfície és proporcional a la massa elevada a 2/3, i com que la pèrdua de calor és proporcional a la superfície, a una creïlla torrada gran li serà més difícil refredar-se que a una de xicoteta. Aquest senzill raonament termodinàmic va portar a concloure que si les pèrdues de calor per la pell són la causa última de la dependència del metabolisme amb la massa, el metabolisme basal hauria de venir donat per una llei de potències d’exponent 2/3.

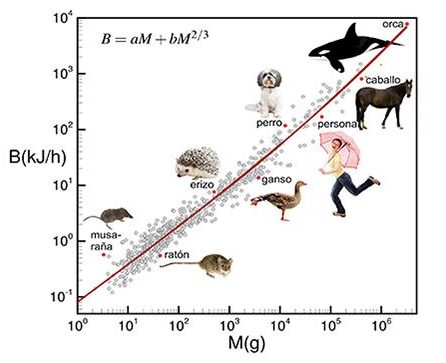
Però Max Kleiber en 1932, amb una mostra àmplia de mesures de metabolisme basal, va veure que les dades pareixien encaixar millor amb la massa elevada a una potència de 3/4 en lloc de 2/3. Aquest inesperat resultat va propiciar una intensa recerca d’explicacions alternatives de l’origen del metabolisme basal, així com un viu debat entre els defensors de l’exponent 2/3 i els del 3/4 que va durar diverses dècades. Cal tenir en compte que la diferència relativa entre els dos valors no és molt alta, només un 12%, amb la qual cosa junt amb la dificultat d’obtenir dades precises que permeteren discriminar entre els dos valors (i la mesura del metabolisme basal d’un animal és certament laboriosa) no hi havia manera de tancar el debat. Fins que Geoffrey West i col·laboradors van elaborar en 1997 un model matemàtic amb què aparentment li posaven fi. Aquest model es basa en el fet que la xarxa de subministraments dels organismes (vasos sanguinis, bronquis, etc.) és el vertader factor limitador del funcionament de l’organisme, i per tant del metabolisme. I aquesta xarxa té una estructura fractal la superfície exterior de la qual escala amb el volum justament com una potència 3/4.

Aquest influent article publicat en la revista Science va aconseguir elevar en certa manera el resultat empíric de Kleiber al rang de llei. Però a mesura que es feien noves mesures i es millorava la precisió, l’explicació fractal va començar a fer aigua. Els resultats empírics acumulats qüestionaven la validesa universal de l’exponent 3/4 en trobar-se classes d’animals que encaixaven millor amb altres exponents, oscil·lant entre 1 (com en els insectes) i 2/3 (en el cas de les aus). I en el cas millor conegut, el dels mamífers, en recopilar-se dades per a un major rang de masses (des de musaranyes a balenes) es descobria que el metabolisme basal no seguia en realitat una llei de potències pura. Si haguera sigut així, en representar aquestes dades en l’escala log-log haurien de ser una línia recta amb pendent 3/4, però no obstant això mostren una clara curvatura. Per exemple, quan ens restringim a mamífers de menys d’1 kg les dades quadren molt millor amb un exponent de 2/3, i per a masses per damunt de 50 kg l’exponent s’acosta a 6/7.

Aquests resultats que posen en dubte el model de West han provocat l’aparició d’una plètora de nous models per a explicar aquestes discrepàncies, alguns d’ells modificacions del model original de West; uns altres, models aptes per a casos particulars o ajustos ad hoc sense un clar suport biològic, i molts altres, models realment creatius encara que de complexitat creixent o amb massa paràmetres lliures. La pèrdua del marc de referència mestre que semblava ser el model fractal de West ha deixat un terreny preparat per a un nou debat sobre l’origen de la (ara incorrectament anomenada) llei de Kleiber, i molt de treball pendent per a la navaixa d’Okcham. És necessari un nou marc de referència que siga parsimoniós i ajude a reconciliar resultats tan diversos.

El model que el nostre equip va publicar recentment en Scientific Reports pretén ser aquest nou marc de referència. En certa manera és un retorn a l’explicació tèrmica com a causa última del fenomen. Amb una diferència: un organisme no pot utilitzar tota l’energia que consumeix a generar calor, una fracció ha de destinar-se a “coses útils”, com la síntesi de proteïnes, la divisió cel·lular, els batecs cardíacs…, és a dir, a fer funcionar i mantenir l’organisme. Si tota l’energia consumida es transformara en calor, certament el metabolisme encaixaria amb un exponent 2/3, però aleshores no parlaríem d’un organisme sinó d’una estufa. D’altra banda, si tota l’energia es consumira eficientment, el metabolisme seria directament proporcional al nombre de cèl·lules que s’estan alimentant, és a dir, a la massa M, però inevitablement una part es perd com a calor. En els organismes reals es donen els dos fenòmens, i aquests interpolen entre aquests dos extrems ideals, cada factor ponderat per un pes en funció de la seua importància. És a dir: B = AM + bM^2/3.

Aquest model permet fer diverses prediccions. Per a endoterms de masses baixes, el terme amb exponent 2/3 domina, la qual cosa explica per què els mamífers de dimensió reduïda i les aus (també xicotetes) encaixen millor amb aquest exponent. En canvi, per a masses grans és l’altre terme el que domina i l’exponent s’acosta més a 1. D’altra banda, els mamífers polars tendeixen a ser termodinàmicament ineficients a fi de mantenir-se calents (a través de l’ús de proteïnes com la termogenina), i donen un valor de b més elevat. I, en efecte, els animals polars encaixen millor amb un exponent de 2/3. En canvi, b és baix si la diferència de temperatura entre l’entorn i el cos és reduïda, com en el cas dels ectoterms, la qual cosa produeix que el primer terme siga el dominant i encaixen millor les seues dades amb exponents més pròxims a 1.

El model també permet fer prediccions quantitatives: a partir d’arguments merament termodinàmics, en el nostre article estimem que per a mamífers la fracció de la ingesta d’energia que no es perd com a calor és com a mitjana d’un 21%. D’altra banda, sabem que la síntesi d’ATP a partir de glucosa (el procés dominant en les condicions sota les quals es mesura el metabolisme basal) només captura el 42% de l’energia, perdent-se la resta per calor, i el posterior ús d’ATP en reaccions biològiques perd un altre 50% d’aquest 42%, la qual cosa dóna finalment un consum eficient d’un 21%, coincidint amb la predicció del nostre model. Com que aquesta és la fracció que no s’emet com a calor, s’esperaria veure aquesta diferència entre la calorimetria directa (que mesura la producció de calor) i la calorimetria indirecta (consum d’oxigen), encara que rares vegades es prenen ambdues mesures al mateix temps. No obstant això, Alexander Zotin va publicar en 2010 diversos mesuraments conjunts de calorimetria directa i indirecta, a partir dels quals veiem que aquestes diferències oscil·len entre el 13 i el 25%, d’acord amb les nostres prediccions.

És aquest model l’explicació definitiva del perquè varia com varia el metabolisme amb la massa? Tal vegada. Com déiem, hi ha moltes altres explicacions alternatives. I no necessàriament són mútuament excloents; probablement moltes d’elles seran vàlides dins de certs límits. Però el nostre model de balanç entre consum eficient i pèrdua tèrmica és autoconsistent, es basa en principis termodinàmics simples però sòlids i genera prediccions que expliquen quantitativament i qualitativament tota una sèrie de característiques biològiques rellevants. És un marc general sobre el qual totes les peces pareixen per fi encaixar.