L’infinit! Cap qüestió ha commogut tan profundament l’esperit de l’home.
David Hilbert (1862–1943)
Ortega y Gasset descrivia l’home com un ésser llançat al món. La nostra arribada sobtada no ve acompanyada d’un llibre d’instruccions, no portem amb nosaltres un breu pamflet informatiu que ens guie en la comprensió d’aquest escenari al qual hem sigut llançats. En aquest panorama, en aquest aterratge brutal, l’home es veurà condemnat i beneït a preguntar, a qüestionar-se insaciablement per ell mateix i per tot el que l’envolta. Hi ha una pregunta que resulta pràcticament inevitable quan l’home aguaita fascinat l’abisme estrellat sobre el seu cap: què hi ha després? Si al xiquet que planteja aquesta pregunta se li responguera, inevitablement se l’estaria convidant a fer una segona pregunta: i després d’això? La infinitud de l’univers constitueix un leitmotiv en la història de les inquietuds de filòsofs i científics.
El primer pas d’aquest breu viatge el farem en l’Antiga Grècia: Anaximandre, deixeble de Tales de Milet, va mirar de descobrir en les seues reflexions la naturalesa de l’arché, el principi de totes les coses. El seu mestre, considerat el primer filòsof d’Occident, va establir que aquest element primer era l’aigua. Anaximandre, amb tot, va donar un tractament més complex a l’arché. En paraules de Diògenes Laerci: “Anaximandre de Milet, fill de Praxíades, va afirmar que el principi i l’element és l’il·limitat, sense definir-lo com a aire, aigua o alguna altra cosa …”.

Gravat que apareix a L’Atmosphere: Météorologie Populaire (París, 1888) de Camille Flammarion
D’Arquites de Tàrent, matemàtic pitagòric que va viure entre els segles V i IV abans de Crist, ens conta Simplici que es plantejava si, trobant-se en el límit del cel dels estels fixos, podia o no estendre la mà fora. L’opció de no poder estendre la mà li resultava absurda, però el fet de poder fer-ho anul·lava aquell espai com a límit últim.
No sols els grecs van plantejar la infinitud del món. Un dels molts mites de l’Antic Egipte que donen compte de la història de l’univers estableix que, en un primer estadi, aquest no era sinó un immens oceà al qual no era possible buscar límits ni dalt ni baix ni pels costats, ni tan sols hi havia dimensions, només una profunditat sense límit.
Si bé la infinitud de l’univers i els conflictes que planteja havia constituït, com hem vist, un terreny comú per a diversos autors de l’antiguitat, amb Aristòtil, això no obstant, l’univers passa a tancar-se, amb límits clars, i serà així durant molt de temps a causa de la contundent influència de l’estagirita en el pensament posterior.
En “Sobre el cel”, “Física” i “Sobre la generació i la corrupció” exposa Aristòtil una cosmologia impregnada de tints platònics. L’univers aristotèlic és finit i etern, i està dividit en dos nivells: el nivell sublunar i el nivell supralunar. El primer està format pels quatre elements (terra, aigua, aire i foc) i participa dels processos de generació i corrupció; el segon està format per “quinta essència”, un element incorruptible i etern, i participa únicament del moviment circular perfecte. El nivell supralunar acaba en l’esfera dels estels fixos, límit últim de l’univers.
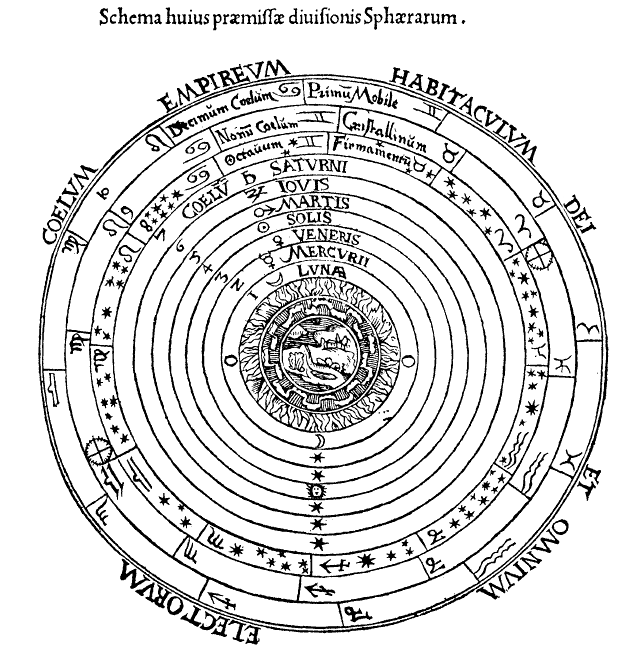
El sistema del món d’Aristòtil en un gravat de Peter Apian a Cosmographia (1524).
L’univers finit d’Aristòtil, vinculat durant l’edat mitjana amb els dogmes cristians, va constituir un bastió difícil d’assaltar. Giordano Bruno, poeta, astrònom i teòleg, hagué de considerar que la infinitud de Déu hauria de traslladar-se a la seua creació. Bruno seria acusat d’heretgia en 1592, i la seua afirmació de la infinitud de l’univers constituiria un dels càrrecs de l’acusació. Bruno es va negar a retractar-se d’aquesta i d’altres huit proposicions, i fou cremat viu al Campo di Fiori, de Roma, el 17 de febrer de 1600.
Un nom indispensable en aquesta exposició és el de Thomas Digges (1546-1595), matemàtic i astrònom anglés. Digges va rebutjar en la seua particular cosmologia la idea de l’esfera fixa d’estels i va postular un nombre infinit d’estels separats per distàncies variables. Digges va tractar d’establir la paral·laxi de la supernova observada per Tycho Brahe (1546-1601) en 1572, i acabaria per exposar que aquesta es trobava més enllà de la Lluna. Açò plantejava una revolució enfront de la visió tradicional segons la qual res es transformava en l’esfera dels estels fixos, cap canvi es contemplava en aquest nivell cosmològic.
Copèrnic no es va endinsar en explicacions al voltant de què podia haver-hi més enllà de l’esfera dels estels fixos. Digges, amb tot, s’atreveix a afirmar que l’univers és infinit i que conté un nombre també infinit d’estels. La frase exacta amb què Digges va obrir les portes d’aquesta nova consideració es troba en el capítol 8 dels apèndixs de la revisió que Digges va realitzar de l’almanac estel·lar de son pare: “this orb of starres fixed infinitely up”.
Amb Digges es va obrir una fissura ferma en el model aristotèlic, i la infinitud de l’univers va començar a ser considerada amb força.
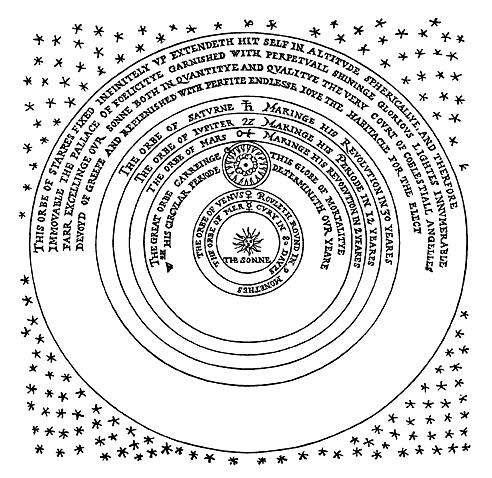
El sistema heliocèntric copernicà en un gravat de Thomas Digges en Perfit Description of the coelestiall orbes (1526)
Què en diu la ciència actual?
És possible que l’univers siga, espacialment, infinit. No obstant això, en el model cosmològic comunament acceptat, el Big Bang, l’univers va nàixer fa uns 13800 milions d’anys. El que la llum ha pogut viatjar en aqueix temps es converteix en el nostre horitzó còsmic; tot el que estiga més enllà, però, no pot sinó limitar-se al pla de l’especulació. L’univers en el seu conjunt no és, per tant, encara accessible. És possible, tot i això, fer-se una idea de la grandària d’aquest univers? Com expliquem en aquest vídeo de conec.es amb guió de Fernando Ballesteros hi ha una forma d’acostar-se a aquesta dada: si mirem l’horitzó que s’estén des del capdamunt d’una muntanya, ens serà difícil donar compte de la seua curvatura, però no en un cos molt més menut que la Terra, com podria ser un asteroide. En un petit asteroide, com el planeta d’El petit príncep d’Antoine de Saint-Exupéry (1900-1944), la curvatura de l’horitzó es fa totalment evident, en tant que s’assembla en dimensions al mateix asteroide. Si l’univers observable fóra només un poc més menut que l’univers real, la seua geometria hauria de presentar una curvatura evident. Tanmateix, no s’esdevé tal cosa, i això indica que l’univers és molt més gran que l’univers observable. Si bé sabem això, no hi ha manera d’establir, limitats com estem al nostre horitzó visual, la magnitud de l’univers real. Podria ser milions de vegades més gran que l’univers observable, podria ser infinit, senzillament no ho sabem.
Més informació: Vegeu l’entrevista d’Alberto Fernández Soto apareguda en conec.es





No comments yet.